¿Qué es un punto?
Un punto muestra una ubicación y como tal, no tiene tamaño o dimensión alguna. Un punto es representado precisamente por eso: un punto y su notación se hace convencionalmente por una letra mayúscula que se escribe en su cercanía.
¿Qué es una recta?
Una recta puede definirse como un conjunto de puntos que se extienden alineados,infinitamente, en dos direcciones opuestas. Una recta es unidimensional y tiene “ancho”. Se la identifica nombrando dos puntos que estén contenidos en ella, o (muy convencionalmente usada esta notación en los salones de clases) nombrándola con una letra minúscula.
¿Qué es un plano?
Un plano es una superficie plana que no tiene dimensión en “volumen” y que se extiende infinitamente en todas las direcciones. Se trata, entonces, de un objeto bi dimensional. En los salones de clase, suele dibujarse como paralelogramo y en general, para diferenciarlo de las notaciones anteriores, se elige nombrarlo con una letra griega, escrita en uno de sus rincones. Si bien se utiliza un paralelogramo (porque de alguna manera hay que dibujarlo) es importante recordar que un plano geométrico es infinito en todas direcciones, no tiene límites y por razones de simplicidad, deberías pensar en un plano como una hoja de papel infinitamente grande.
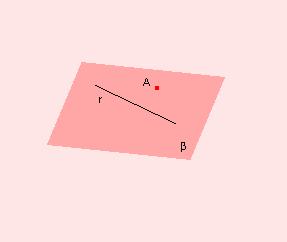
Veamos estos tres conceptos y sus respectivas notaciones a través del siguiente dibujo:
En esta figura podemos apreciar a los tres elementos que mencionamos con sus notaciones respectivas. Por una parte el punto A, por otra a la recta r (de la cual no forma parte el punto A) y por último al plano β (beta).
Estos tres elementos básicos, servirán -como señalé antes- para elaborar la totalidad de la Geometría como la conocemos hoy en día, desde la Geometría plana a la Geometría espacial. Los primeros conceptos son los llamados Axiomas fundamentales de la Geometría plana; a ellos estará dedicado nuestro próximo post. Te invito a estar pendiente.